Bài 6.1. Giới thiệu về heap
Nội dung bài học
Khái niệm và đặc điểm
- Heap-đống là một cấu trúc dữ liệu đặc biệt dựa trên cây. Trong đó cây là một cây hoàn chỉnh thỏa mãn tính chất của đống:
- Trong max heap, bất kì node cha nào đều có giá trị lớn hơn hoặc bằng giá trị các node con của nó.
- Trong min heap, bất kì node cha nào đều có giá trị nhỏ hơn hoặc bằng giá trị của các node con của nó.
- Node trên cùng của heap gọi là node gốc và là node có giá trị lớn nhất trong max heap, nhỏ nhất trong min heap.
- Triển khai phổ biến của heap là binary heap dựa trên cây nhị phân.
- Heap được sử dụng trong triển khai hàng đợi ưu tiên. Ta thường gọi hàng đợi ưu tiên là heap cho dù chúng được triển khai theo cách nào.
- Đống có vai trò đặc biệt trong các thuật toán cho đồ thị như thuật toán Dijkstra hay trong heap sort.
- Không nhầm lẫn heap trong cấu trúc dữ liệu và heap-chỉ vùng nhớ được cấp phát cho đối tượng trong cấp phát bộ nhớ động.
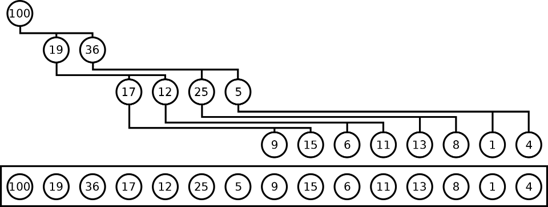
- Ta thường sử dụng mảng để triển khai heap, trong đó:
- Mỗi phần tử mảng đại diện cho một node của heap.
- Mối liên hệ giữa hai node cha, con được thể hiện qua chỉ số của phần tử mảng.
- Phần tử đầu tiên của mảng là node gốc, hai vị trí tiếp theo là hai node con của node gốc. 4 vị trí kế tiếp là 4 node con của hai node phía trên.
- Như vậy, cho node ở vị trí i, hai node con của nó sẽ nằm ở vị trí 2i+1 và 2i+2. Node cha của nó sẽ ở vị trí phần nguyên của [(i-1)/2].
- Việc cân bằng heap được thực hiện bằng các thao tác sàng lên hoặc xuống – tức tráo đổi các phần tử không đúng vị trí.
- Sau khi thực hiện thêm mới hoặc xóa phần tử khỏi heap, các phần tử trong heap sẽ mất tính chất vốn có của nó.
- Để tái cân bằng lại heap, ta thực hiện việc tráo đổi các phần tử của heap.
Các thao tác trên heap
- Tạo heap.
- Trộn(hợp) hai heap.
- Tìm giá trị min/max trong heap.
- Chèn thêm phần tử vào heap.
- Thay thế node trong heap.
- Xóa node khỏi heap.
- Đếm số phần tử hiện có của heap.
- Kiểm tra heap có rỗng không.
- Sàng lên/xuống: di chuyển node lên trên hoặc xuống dưới.
Các biến thể của heap
- Đống nhị phân
- Đống nhị thức
- Đống ghép
- Đống Fibonacci
- Đống mềm
- Đống chỉ số
- Và nhiều loại đống khác, trong đó ta tập trung chủ yếu vào đống nhị phân.
Ứng dụng của heap
- Sau đây là một số ứng dụng của heap:
- Heapsort: một trong những thuật toán sắp xếp tốt nhất.
- Các thuật toán lựa chọn: thực hiện với thời gian hằng số.
- Các thuật toán đồ thị: có thời gian chạy đa thức. Ví dụ trong thuật toán tìm đường đi ngắn nhất, thuật toán cây bao trùm tối thiểu.
- Hàng đợi ưu tiên: triển khai bằng heap.
- K-way merge: trộn k luồng đầu vào đã sắp xếp thành 1 luồng sắp xếp.
- Thống kê thứ tự: sử dụng heap để tìm phần tử lớn hoặc nhỏ thứ k trong mảng một cách hiệu quả.