Bài 8.2. Thuật toán bubble sort
Nội dung bài học
Mục đích sử dụng
- Sắp xếp là việc đặt các phần tử của một tập hợp theo thứ tự với một hoặc một số tiêu chí nào đó. Ví dụ từ giá trị lớn nhất đến nhỏ nhất, tên A-Z trong bảng chữ cái.
- Sắp xếp một tập hợp là chức năng thiết yếu có trong hầu hết các ứng dụng, phần mềm. Do đó ta cần nắm được một số các thuật toán sắp xếp cơ bản để vận dụng vào sản phẩm ta đang triển khai.
- Việc sắp xếp sẽ giúp tối ưu chương trình, chuẩn hóa dữ liệu đầu vào, tạo đầu ra dễ đọc hiểu với con người.
- Ví dụ ta cần tìm ra top những người có tầm ảnh hưởng nhất thế giới của năm nay.
- Hay ta cần sắp xếp danh sách sinh viên trong lớp theo thứ tự tên tăng dần A-Z.
- Hoặc ta cần sắp xếp danh sách nhân viên của một công ty theo mức lương giảm dần từ cao nhất đến thấp nhất.
- Các trang web bán hàng thường có chức năng sắp xếp các sản phẩm mà họ đang kinh doanh theo giá bán từ cao đến thấp hoặc từ thấp đến cao chẳng hạn.
Sắp xếp tăng dần
- Thuật toán sắp xếp nổi bọt có độ phức tạp trung bình là O(n^2). Thuật toán có độ phức tạp càng lớn thì sắp xếp càng chậm và càng kém hiệu quả.
- Sau đây là mã giả của thuật toán sắp xếp nổi bọt theo thứ tự các phần tử có giá trị nhỏ nhất được tìm ra và đặt vào đúng vị trí của nó trong tập hợp(mảng) trước:
function bubbleSort(arr[]){ // arr-mảng 1 chiều, n: số phần tử của mảng
n = arr.length // lấy số phần tử của mảng
for (i from 0 to n - 2){ // cho i chạy từ 0 đến n-2
for (j from n - 1 to i + 1){ // cho j chạy từ n-1 đến i+1
<span style="color: #800000;"><strong>if (arr[j - 1] > arr[j]){</strong></span> // nếu phần tử đứng trước lớn hơn phần tử đứng sau, đổi chỗ hai phần tử
tmp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = tmp;
} // end if
} // end inner for loop
} // end outer for loop
} // end function- Triển khai:
// T là kiểu có thể so sánh các đối tượng của nó với nhau
public static <T extends Comparable<T>> void bubbleSort(T[] arr) {
int n = arr.length;
for (int i = 0; i <= n - 2; i++) {
for (int j = n - 1; j >= i + 1; j--) {
if (arr[j - 1].compareTo(arr[j]) > 0) {
T tmp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = tmp;
}
}
}
}- Hình minh họa các bước thực hiện đổi chỗ phần tử trong mảng.
- Giá trị ban đầu của mảng: 5 4 1 6 9 7 3 2.
- Hai ô màu xanh nhạt liền kề thể hiện việc tráo đổi giá trị.
- Hai ô màu đỏ nhạt liền kề thể hiện việc không xảy ra tráo đổi.
- Ô màu xanh đậm thể hiện giá trị đã được đưa vào đúng vị trí của nó.
- Mũi tên trên đầu thể hiện vị trí của chỉ số i, j tại thời điểm thuật toán đang hoạt động.
- Kết quả, các phần tử mảng phân bố tăng dần theo giá trị tính từ trái sang phải: 1 2 3 4 5 6 7 9.
- Với i = 0, 1:
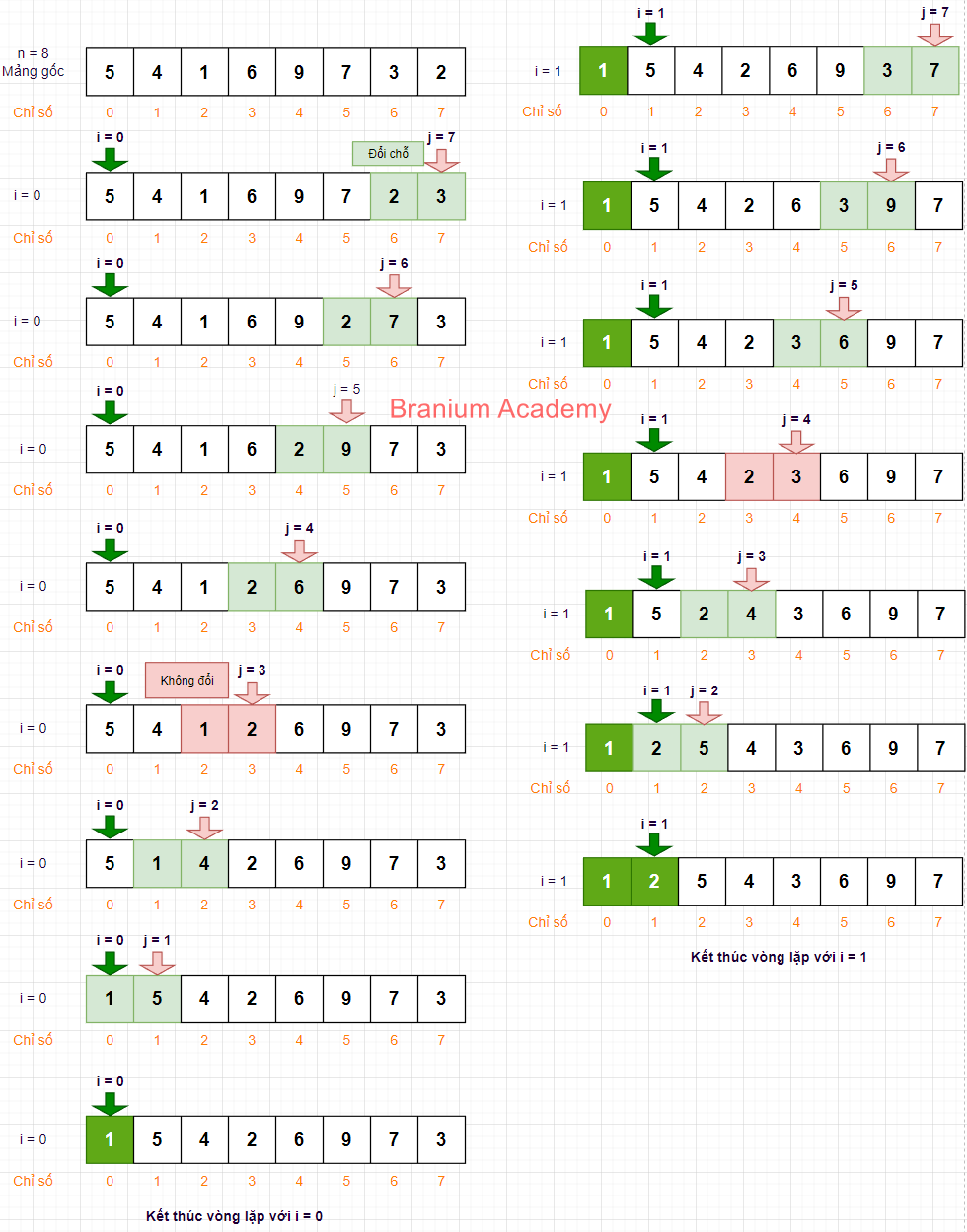
- Với i = 2, 3:
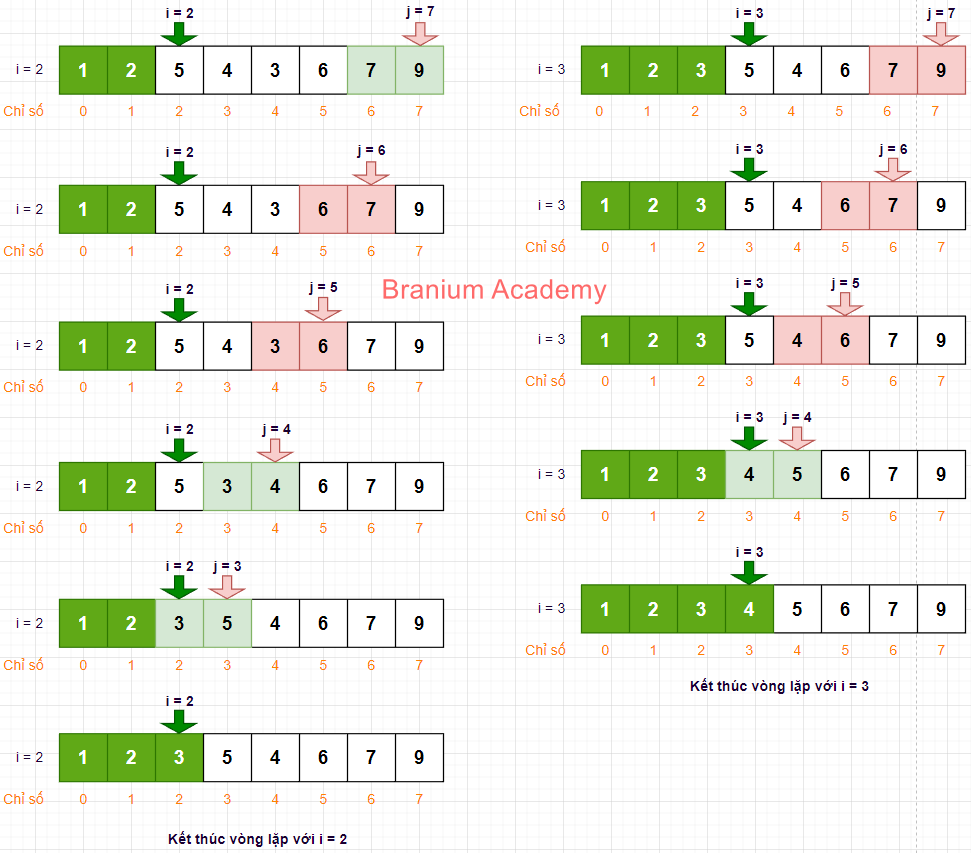
- Với i = 4, 5, 6:
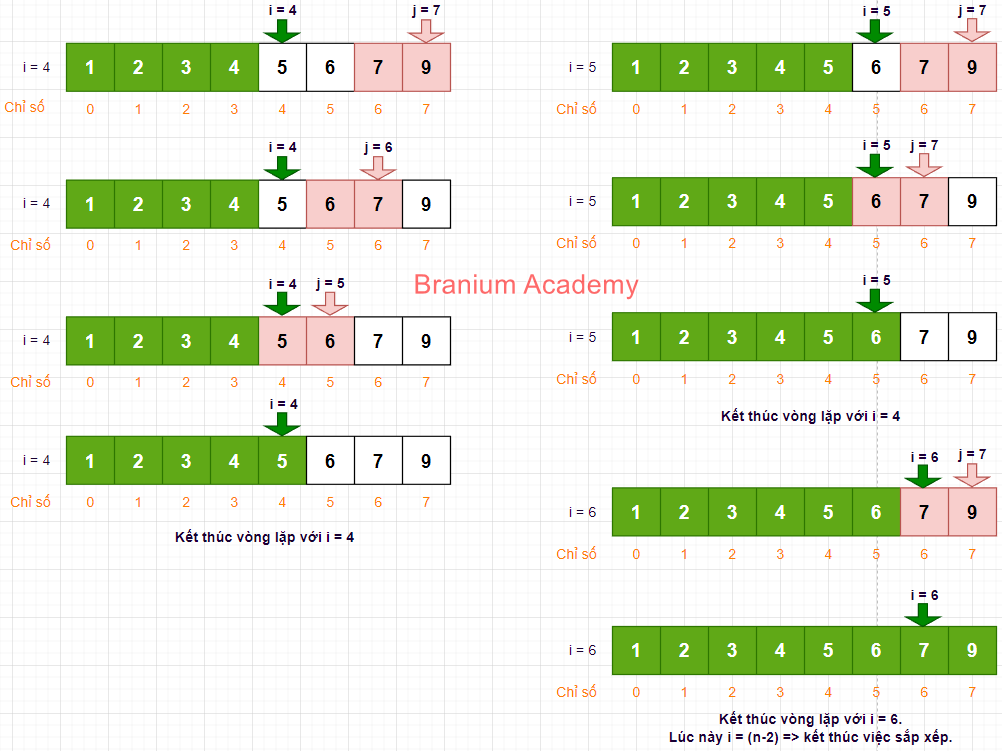
Sắp xếp giảm dần
- Để sắp xếp giảm dần, ta chỉ cần đổi điều kiện từ arr[j-1] > arr[j] thành arr[j-1]<arr[j].
function bubbleSort(arr[]){ // arr-mảng 1 chiều, n: số phần tử của mảng
int n = arr.length; // lấy số phần tử của mảng
for (i from 0 to n - 2){ // cho i chạy từ 0 đến n-2
for (j from n - 1 to i + 1){ // cho j chạy từ n-1 đến i+1
<span style="color: #800000;"><strong>if (arr[j - 1] < arr[j]){</strong></span> // nếu phần tử đứng trước nhỏ hơn phần tử đứng sau, đổi chỗ hai phần tử
tmp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = tmp;
} // end if
} // end inner for loop
} // end outer for loop
} // end function- Code mẫu:
public static <T extends Comparable<T>> void bubbleSortDESC(T[] arr) {
int n = arr.length;
for (int i = 0; i <= n - 2; i++) {
for (int j = n - 1; j >= i + 1; j--) {
if (arr[j - 1].compareTo(arr[j]) < 0) {
T tmp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = tmp;
}
}
}
}Thuật toán buble sort tối ưu
- Trong trường hợp nếu lần duyệt nào đó với một biến chạy i cố định mà khi vòng lặp bên trong với j kết thúc, không xảy ra việc đổi chỗ cặp phần tử nào tức là các cặp số liền kề nhau đã sắp xếp đúng thứ tự. Do đó ta có thể dùng một cờ đánh dấu để kiểm soát việc lặp của trường hợp này.
- Sau đây là mã giả cho thuật toán buble sort tối ưu:
function bubbleSortOpt(arr[]) { // thuật toán tối ưu
n = arr.length; // lấy số phần tử của mảng arr
isSwapped: boolean // biến đánh dấu có xảy ra đổi chỗ ở vòng lặp hiện tại
i = n - 1 // ban đầu i = n - 1
while (i > 0) {
isSwapped = false // giả định không xảy ra sắp xếp trong vòng lặp hiện tại
for (j from 0 to i - 1) { // cho j chạy từ 0 đến i - 1
if (arr[j] > arr[j + 1]) { // nếu phần tử đứng trước nhỏ hơn phần tử đứng sau
swap(arr[j], arr[j + 1]) // đổi chỗ hai phần tử này
isSwapped = true // đánh dấu rằng đã xảy ra việc đổi chỗ hai phần tử
}
}
if (isSwapped == false) { // nếu kết thúc vòng lặp với j mà không xảy ra sự đổi chỗ
break // kết thúc việc sắp xếp, vì tập hợp đã có thứ tự như mong muốn
}
else { // ngược lại
i-- // giảm i, tiếp tục việc sắp xếp trong vòng lặp kế tiếp
}
}
}- Code mẫu:
public static <T extends Comparable<T>> void bubbleSortOpt(T[] arr) {
int n = arr.length;
boolean isSwapped;
int i = n - 1;
while (i > 0) {
isSwapped = false;
for (int j = 0; j <= i - 1; j++) {
if (arr[j].compareTo(arr[j + 1]) > 0) {
T tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
isSwapped = true;
}
}
if (!isSwapped) {
break;
} else {
i--;
}
}
}Code mẫu hoàn chỉnh:
public class BubbleSort {
public static <T extends Comparable<T>> void bubbleSort(T[] arr) {
int n = arr.length;
for (int i = 0; i <= n - 2; i++) {
for (int j = n - 1; j >= i + 1; j--) {
if (arr[j - 1].compareTo(arr[j]) > 0) {
T tmp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = tmp;
}
}
}
}
public static <T extends Comparable<T>> void bubbleSortDESC(T[] arr) {
int n = arr.length;
for (int i = 0; i <= n - 2; i++) {
for (int j = n - 1; j >= i + 1; j--) {
if (arr[j - 1].compareTo(arr[j]) < 0) {
T tmp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = tmp;
}
}
}
}
public static <T extends Comparable<T>> void bubbleSortOpt(T[] arr) {
int n = arr.length;
boolean isSwapped;
int i = n - 1;
while (i > 0) {
isSwapped = false;
for (int j = 0; j <= i - 1; j++) {
if (arr[j].compareTo(arr[j + 1]) > 0) {
T tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
isSwapped = true;
}
}
if (!isSwapped) {
break;
} else {
i--;
}
}
}
public static void main(String[] args) {
Integer[] arr1 = {2, 1, 5, 0, 3, 4, 0, 9, 8, 7, 6, 5};
Integer[] arr2 = {4, 15, 20, 9, 8, 7, 6, 5, 74, 12};
Integer[] arr3 = {6, 50, 87, 10, 25, 14, 2, 8, 33, 69};
System.out.println("Trước khi sắp xếp: ");
showElements(arr1);
showElements(arr2);
showElements(arr3);
bubbleSortOpt(arr1, arr1.length);
bubbleSort(arr2, arr2.length);
bubbleSortDESC(arr3, arr3.length);
System.out.println("Sau khi sắp xếp: ");
showElements(arr1);
showElements(arr2);
showElements(arr3);
}
private static <T> void showElements(T[] arr) {
for (var e : arr) {
System.out.print(e + " ");
}
System.out.println("\n----------------------------");
}
}// kết quả: Trước khi sắp xếp: 2 1 5 0 3 4 0 9 8 7 6 5 ---------------------------- 4 15 20 9 8 7 6 5 74 12 ---------------------------- 6 50 87 10 25 14 2 8 33 69 ---------------------------- Sau khi sắp xếp: 0 0 1 2 3 4 5 5 6 7 8 9 ---------------------------- 4 5 6 7 8 9 12 15 20 74 ---------------------------- 87 69 50 33 25 14 10 8 6 2 ---------------------------- Process finished with exit code 0
Bài tập thực hành
- Tải đề bài: nhấn vào đây
- Bài giải mẫu: nhấn vào đây

